As we know, being “good in maths” is something of a talent some people possess. For some, mathematics is easy to understand and for others, it is a real nightmare!
Some scientists believe that our brain is not created for the purpose of doing mathematics and this is one of the main reasons why many children face difficulties when handling mathematics. It is believed that our brain is not made to work as a computer – the world around us is not based on numbers. Instead – numbers have been invented to explain our physical surroundings.
The different ways we perceive mathematics
As with colors, people perceive and imagine numbers differently. Some find it easy to adopt the numerical way we denote quantities. They work with numbers in their head and have no problems solving mathematical problems. Others see quantities in volumes – for example, when you speak to them about the 3 bottles of milk you bought yesterday, they will not imagine the number 3, but the bottles of milk one next to another.
Because of this different perception, a lot of maths teachers try different methods of illustrating mathematical operations. One of the most peculiar methods turns out to be the Chinese method of multiplication called Sticks and Squirrels.
The Chinese method – lattice multiplication
You can meet this method under different names – although the most common one is Sticks and Squirrels, some may call it lattice multiplication, Japanese multiplication or even stick method. It doesn’t really matter what you call it, what matters is that this method is fun, easy, and actually works!
So how does it actually work? Let’s have a quick tutorial on the Chinese method of multiplication.
Let us start with an easy problem:
2×2= ?

The Chinese method suggests we use lines or as children call them “sticks” to illustrate how the numbers interact. Every number has its lines on its own plane:
What we do here is count how many times the lines intersect. In this case – it is four.
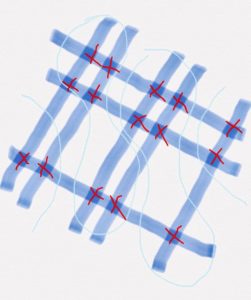
So let us try something more difficult:
22×22= ?

As in this example, the number is bigger, we will be having lines, illustrating the ones and lines illustrating the tens. Then we see that we have to divide the places where the lines intersect into sections. The first section starting right to left is the section illustrating ones (there we can count 4 intersections). The second vast section is the tens (the number of intersections is 8). And, as you probably already guessed, the third section is the hundreds (we have 4 intersections). Using this technique we got the number 484. Check your calculator!
This can go on with even very large numbers:
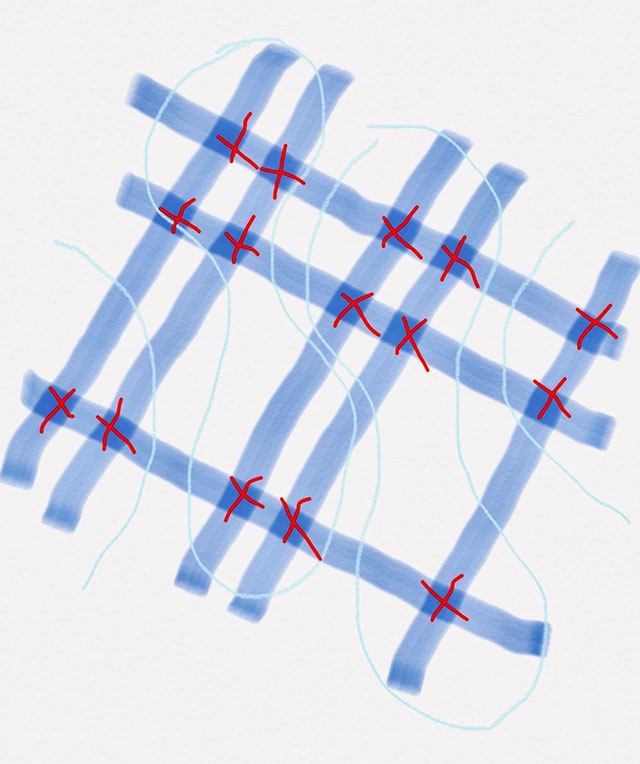
221×12= ?
We have three sets of lines for the number 221 and two more sets of lines for the number 12. Properly separating the sections for ones, tens, hundreds and thousands, and counting the places of intersections we receive the number 2652. You’re free to use your calculator again and see for yourself that this lattice multiplication method is actually effective!
There’s quite a lot of people who refer to the Sticks and Squirrels as the “Chinese multiplication trick”, but as you can see – this is no trick at all! Building a deep, conceptual understanding of such techniques helps kids view mathematics differently. It shows them that maths is not only efficient but fun as well!